Randomness and Noise - Metal Shaders

The Texture of Reality

Look at concrete. Wood grain. Clouds. Your skin. Nothing in nature is perfectly smooth or perfectly patterned. The universe has texture - subtle variations that make materials feel real rather than computer-generated.

Here's the paradox: computers can't generate true randomness, yet they must simulate the organic randomness of nature. The solution? Deterministic chaos - mathematical functions that produce results so complex they appear random, yet remain perfectly reproducible.

This chapter reveals how to add the imperfections that make perfection.

The Fundamental Problem: Why random() Doesn't Exist in Shaders

In CPU programming, you can call random() and get a different value each time. In shaders, this is impossible. Why?

Remember: Every pixel executes the same function simultaneously. If random() existed, either:

Every pixel would get the same "random" value (useless)
Results would change every frame (flickering chaos)
Adjacent pixels couldn't coordinate (no smooth gradients)

The solution is beautiful: We create functions that look random but are actually deterministic hash functions.

Mathematical Foundation: The Art of Fake Randomness

The Classic Hash Function

float random(float2 st) {
    return fract(sin(dot(st, float2(12.9898, 78.233))) * 43758.5453);
}

Let's dissect this magic:

// Step 1: dot product creates a single value from 2D input
float dotProduct = dot(st, float2(12.9898, 78.233));
// For st = (1,1): 12.9898 + 78.233 = 91.2228

// Step 2: sin() creates oscillation (-1 to 1)
float sineValue = sin(dotProduct);
// sin(91.2228) = some value between -1 and 1

// Step 3: Multiply by large prime number
float amplified = sineValue * 43758.5453;
// Amplifies tiny differences in sine values

// Step 4: fract() keeps only decimal part (0-1)
float result = fract(amplified);
// Ensures output is always 0-1 range

The magic numbers (12.9898, 78.233, 43758.5453) aren't special - they're just chosen to create good distribution. The pattern is what matters: input → nonlinear transform → amplify differences → normalize range.

Building Your First Noise Shader

Random Noise

Digital static - a grid of random grayscale values demonstrating basic hash-based randomness

[[ stitchable ]] half4 randomNoise(float2 position, half4 color, float2 size) {
  // Convert to UV coordinates (normalized 0-1 range, explained in Chapter 2)
  float2 uv = position / size;

  // Scale up to see individual random values
  float2 scaledUV = uv * 10.0;

  // Get the integer part (which cell we're in)
  float2 cellID = floor(scaledUV);

  // Generate random value for this cell
  float randomValue = fract(sin(dot(cellID, float2(12.9898, 78.233))) * 43758.5453);

  return half4(randomValue, randomValue, randomValue, 1.0);
}

SwiftUI Metal Shader

This creates a grid of random gray values - digital static. Not very useful yet.

The Revolution: Gradient Noise (Perlin's Insight)

Ken Perlin's Academy Award-winning breakthrough wasn't just creating random values - it was creating smooth transitions between random values. This innovation revolutionized computer graphics.

Value Noise: The Smooth Random

Smooth Noise (Value Noise)

Smooth interpolation between random values creates organic, cloud-like patterns - the foundation of natural textures

// Generate smooth noise by interpolating between random values
float valueNoise(float2 st) {
  // Grid coordinates
  float2 i = floor(st);  // Integer (cell) position
  float2 f = fract(st);  // Fractional position within cell

  // Four corners of current cell
  float a = random(i);                        // Bottom-left
  float b = random(i + float2(1.0, 0.0));    // Bottom-right
  float c = random(i + float2(0.0, 1.0));    // Top-left
  float d = random(i + float2(1.0, 1.0));    // Top-right

  // Smooth interpolation curves (better than linear!)
  float2 u = f * f * (3.0 - 2.0 * f);  // Smoothstep curve

  // Bilinear interpolation
  float bottom = mix(a, b, u.x);  // Interpolate bottom edge
  float top = mix(c, d, u.x);     // Interpolate top edge
  return mix(bottom, top, u.y);   // Interpolate between edges
}

[[ stitchable ]] half4 smoothNoise(float2 position, half4 color, float2 size) {
  float2 uv = position / size;

  // Scale for visible noise pattern
  float noiseScale = 8.0;
  float noise = valueNoise(uv * noiseScale);

  return half4(noise, noise, noise, 1.0);
}

SwiftUI Metal Shader

Multi-Octave Noise: The Secret to Natural Textures

Nature doesn't have just one scale of detail. Mountains have overall shape, smaller peaks, rocks, pebbles, and grains of sand. We simulate this with octaves:

Fractal Noise (Multi-Octave)

Layering multiple scales of noise creates complex, natural-looking textures with detail at every zoom level - animated for realism

[[ stitchable ]] half4 fractalNoise(
  float2 position,
  half4 color,
  float2 size,
  float time
) {
  float2 uv = position / size;

  float value = 0.0;      // Accumulated noise value
  float amplitude = 1.0;   // Strength of each octave
  float frequency = 1.0;   // Scale of each octave

  // Add 6 octaves of noise
  for(int i = 0; i < 6; i++) {
      // Add noise at current frequency and amplitude
      value += amplitude * valueNoise(uv * frequency * 4.0 + time * 0.1);

      // Each octave is twice as detailed but half as strong
      frequency *= 2.0;   // Double the frequency (smaller details)
      amplitude *= 0.5;   // Halve the amplitude (less influence)
  }

  // Normalize (sum of amplitudes: 1 + 0.5 + 0.25 + ... ≈ 2)
  value /= 2.0;

  return half4(value, value, value, 1.0);
}

SwiftUI Metal Shader

Advanced Noise Types

Gradient Noise (True Perlin Noise)

Instead of interpolating random values, Perlin noise interpolates random gradients:

// Generate random gradient vector for a grid point
float2 randomGradient(float2 p) {
    // Random angle
    float angle = random(p) * 6.28318530718;  // 2π
    return float2(cos(angle), sin(angle));
}

float gradientNoise(float2 st) {
    float2 i = floor(st);
    float2 f = fract(st);
    
    // Calculate gradients at four corners
    float2 g00 = randomGradient(i);
    float2 g10 = randomGradient(i + float2(1.0, 0.0));
    float2 g01 = randomGradient(i + float2(0.0, 1.0));
    float2 g11 = randomGradient(i + float2(1.0, 1.0));
    
    // Calculate dot products
    float n00 = dot(g00, f);
    float n10 = dot(g10, f - float2(1.0, 0.0));
    float n01 = dot(g01, f - float2(0.0, 1.0));
    float n11 = dot(g11, f - float2(1.0, 1.0));
    
    // Smooth interpolation
    float2 u = f * f * (3.0 - 2.0 * f);
    
    // Interpolate
    float nx0 = mix(n00, n10, u.x);
    float nx1 = mix(n01, n11, u.x);
    return mix(nx0, nx1, u.y) * 0.5 + 0.5;  // Normalize to 0-1
}

Simplex Noise: The Performance King

Ken Perlin later created Simplex noise - faster and with better properties:

// 2D Simplex noise - more efficient than classic Perlin
float simplexNoise(float2 st) {
    const float F2 = 0.366025404;  // (sqrt(3) - 1) / 2
    const float G2 = 0.211324865;  // (3 - sqrt(3)) / 6
    
    // Skew the input space to determine simplex cell
    float s = (st.x + st.y) * F2;
    float2 i = floor(st + s);
    float t = (i.x + i.y) * G2;
    float2 i0 = i - t;  // Unskew cell origin back to (x,y) space
    float2 x0 = st - i0;  // The x,y distances from cell origin
    
    // Determine which simplex we're in
    float2 i1 = (x0.x > x0.y) ? float2(1.0, 0.0) : float2(0.0, 1.0);
    
    // Calculate corner offsets
    float2 x1 = x0 - i1 + G2;
    float2 x2 = x0 - 1.0 + 2.0 * G2;
    
    // Calculate contributions from three corners
    float n0 = max(0.0, 0.5 - dot(x0, x0));
    n0 = n0 * n0 * n0 * n0 * dot(randomGradient(i0), x0);
    
    float n1 = max(0.0, 0.5 - dot(x1, x1));
    n1 = n1 * n1 * n1 * n1 * dot(randomGradient(i0 + i1), x1);
    
    float n2 = max(0.0, 0.5 - dot(x2, x2));
    n2 = n2 * n2 * n2 * n2 * dot(randomGradient(i0 + 1.0), x2);
    
    // Scale output to [0, 1]
    return 70.0 * (n0 + n1 + n2) * 0.5 + 0.5;
}

Practical Applications

Marble Texture

Realistic marble with flowing veins created by warping sine waves with noise - demonstrates practical material generation

[[ stitchable ]] half4 marbleTexture(
  float2 position,
  half4 color,
  float2 size,
  float time
) {
  float2 uv = position / size;

  // Create flowing marble veins
  float noise = 0.0;
  float frequency = 4.0;
  float amplitude = 1.0;

  // Multiple octaves for detail
  for(int i = 0; i < 4; i++) {
      noise += amplitude * valueNoise(uv * frequency + time * 0.02);
      frequency *= 2.1;  // Slightly non-doubling for more organic look
      amplitude *= 0.5;
  }

  // Create vein pattern with sine
  float marble = sin(uv.x * 10.0 + noise * 10.0) * 0.5 + 0.5;

  // Color: white marble with gray veins
  half3 white = half3(0.95, 0.95, 0.9);
  half3 gray = half3(0.4, 0.4, 0.45);
  half3 marbleColor = mix(gray, white, marble);

  return half4(marbleColor.r, marbleColor.g, marbleColor.b, 1.0);
}

SwiftUI Metal Shader

Animated Clouds

Cloudy Skies

Realistic animated clouds using multiple layers of noise moving at different speeds over a sky gradient

[[ stitchable ]] half4 cloudySkies(
  float2 position,
  half4 color,
  float2 size,
  float time
) {
  float2 uv = position / size;

  // Two layers of clouds moving at different speeds
  float clouds1 = 0.0;
  float clouds2 = 0.0;

  // Layer 1: Large, slow clouds
  float2 offset1 = float2(time * 0.01, time * 0.005);
  for(int i = 0; i < 3; i++) {
      float freq = pow(2.0, float(i));
      clouds1 += valueNoise((uv + offset1) * freq * 2.0) / freq;
  }

  // Layer 2: Smaller, faster clouds
  float2 offset2 = float2(time * 0.02, -time * 0.01);
  for(int i = 0; i < 4; i++) {
      float freq = pow(2.0, float(i));
      clouds2 += valueNoise((uv + offset2) * freq * 4.0) / freq;
  }

  // Combine layers
  float cloudDensity = clouds1 * 0.7 + clouds2 * 0.3;
  cloudDensity = smoothstep(0.4, 0.7, cloudDensity);

  // Sky gradient
  float3 skyTop = float3(0.3, 0.5, 0.9);
  float3 skyBottom = float3(0.7, 0.8, 1.0);
  float3 skyColor = mix(skyBottom, skyTop, uv.y);

  // Cloud color
  float3 cloudColor = float3(1.0, 1.0, 1.0);

  // Mix sky and clouds
  float3 finalColor = mix(skyColor, cloudColor, cloudDensity);

  return half4(finalColor.r, finalColor.g, finalColor.b, 1.0);
}

SwiftUI Metal Shader

Wood Grain

Natural wood texture with growth rings and grain detail created by warping sine patterns with noise

[[ stitchable ]] half4 woodGrain(
  float2 position,
  half4 color,
  float2 size
) {
  float2 uv = position / size;

  // Rotate for wood grain direction
  float angle = 0.1;  // Slight angle
  float2 rotatedUV = float2(
      uv.x * cos(angle) - uv.y * sin(angle),
      uv.x * sin(angle) + uv.y * cos(angle)
  );

  // Base wood ring pattern
  float rings = sin((rotatedUV.x + valueNoise(rotatedUV * 3.0) * 0.1) * 30.0);

  // Add fine detail
  float detail = valueNoise(rotatedUV * 50.0) * 0.1;
  float grain = rings + detail;

  // Wood colors
  half3 lightWood = half3(0.7, 0.5, 0.3);
  half3 darkWood = half3(0.4, 0.25, 0.1);

  half3 woodColor = mix(darkWood, lightWood, grain * 0.5 + 0.5);

  return half4(woodColor.r, woodColor.g, woodColor.b, 1.0);
}

SwiftUI Metal Shader

Performance Optimization

Noise Performance Hierarchy (Fastest to Slowest)

Hash-based random: Single calculation per pixel
Value noise: 4 random lookups + interpolation
Gradient noise: 4 gradient calculations + dot products
Simplex noise: 3 corner contributions (better than 4!)
Fractal noise: Multiple octaves multiply cost

Optimization Techniques

// EXPENSIVE: Calculating noise every frame
float noise = valueNoise(uv * 10.0 + time);

// OPTIMIZED: Pre-calculate when possible
float staticNoise = valueNoise(uv * 10.0);  // Calculate once
float animatedPart = sin(time + staticNoise * 2.0);  // Animate the result

// EXPENSIVE: Too many octaves
for(int i = 0; i < 10; i++) {  // 10 octaves is overkill

// OPTIMIZED: Minimum octaves for desired detail
for(int i = 0; i < 4; i++) {   // Usually sufficient

Common Pitfalls

Pitfall 1: Banding in Gradients

// WRONG: Visible stepping in smooth gradients
float noise = floor(valueNoise(uv * 10.0) * 10.0) / 10.0;  // Quantized

// CORRECT: Smooth gradients
float noise = valueNoise(uv * 10.0);

Pitfall 2: Incorrect Noise Scaling

// WRONG: Noise values can exceed 0-1 range
float noise = valueNoise(uv) * 2.0;  // Can be > 1!

// CORRECT: Keep in valid range or clamp
float noise = saturate(valueNoise(uv) * 2.0);

Pitfall 3: Performance Death by Octaves

// WRONG: Exponential performance cost
for(int octave = 0; octave < userOctaves; octave++) {  // Variable loop count

// CORRECT: Fixed, reasonable octave count
const int maxOctaves = 4;
for(int octave = 0; octave < maxOctaves; octave++) {

Challenges

Challenge 1: Static Texture Generator

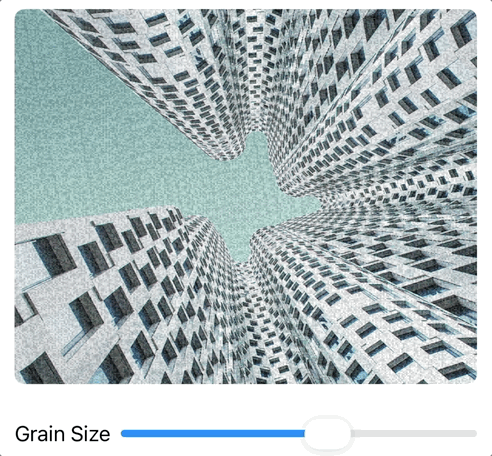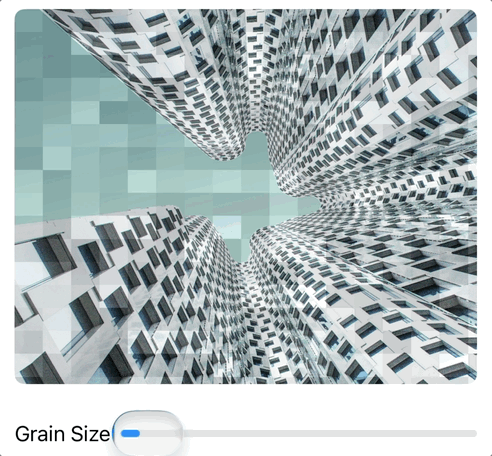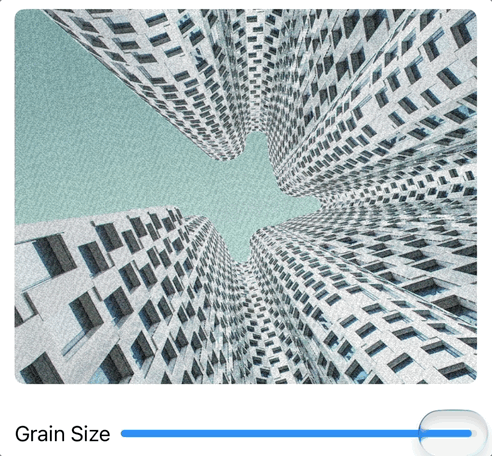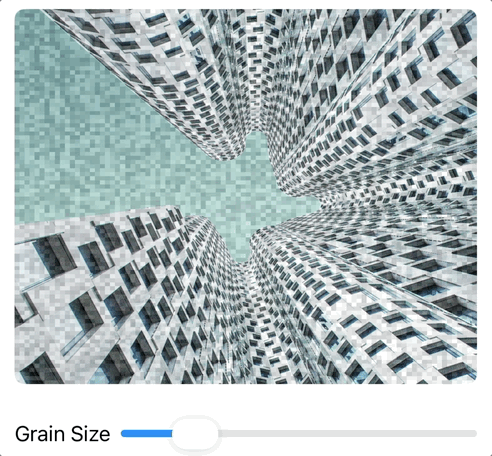
Static Texture Generator Example

Create a shader that generates TV static with controllable "grain size".

SwiftUI Template:

struct StaticTextureView: View {
    @State private var grainSize: Float = 100.0
    
    var body: some View {
        VStack {
            Rectangle() // Or replace with image
                .visualEffect { content, proxy in
                    content.colorEffect(ShaderLibrary.staticTexture(
                        .float2(proxy.size),
                        .float(grainSize)
                    ))
                }
                .frame(height: 300)
            
            HStack {
                Text("Grain Size")
                Slider(value: $grainSize, in: 10...200)
            }
            .padding()
        }
    }
}

Challenge 2: Animated Water Caustics

Animated Water Caustics Example

Create an animated water caustics effect using multiple layers of noise.

SwiftUI Template:

struct WaterCausticsView: View {
    @State private var timeValue: Float = 0.0
    let timer = Timer.publish(every: 1/60.0, on: .main, in: .common).autoconnect()
    
    var body: some View {
        Rectangle()
            .fill(Color.blue.opacity(0.3))
            .visualEffect { content, proxy in
                content.colorEffect(ShaderLibrary.waterCaustics(
                    .float2(proxy.size),
                    .float(timeValue)
                ))
            }
            .frame(height: 400)
            .onReceive(timer) { _ in
                timeValue += 1/60.0
            }
    }
}

Challenge 3: Procedural Fire

Procedural Fire Example

Create a fire effect using noise and color gradients.

SwiftUI Template:

struct ProceduralFireView: View {
    @State private var timeValue: Float = 0.0
    @State private var intensity: Float = 1.0
    let timer = Timer.publish(every: 1/60.0, on: .main, in: .common).autoconnect()
    
    var body: some View {
        VStack {
            Rectangle()
                .fill(Color.black)
                .visualEffect { content, proxy in
                    content.colorEffect(ShaderLibrary.fireEffect(
                        .float2(proxy.size),
                        .float(timeValue),
                        .float(intensity)
                    ))
                }
                .frame(height: 300)
            
            HStack {
                Text("Intensity")
                Slider(value: $intensity, in: 0.5...2.0)
            }
            .padding()
        }
        .onReceive(timer) { _ in
            timeValue += 1/60.0
        }
    }
}

Challenge 4: Touch Particle System (Advanced)

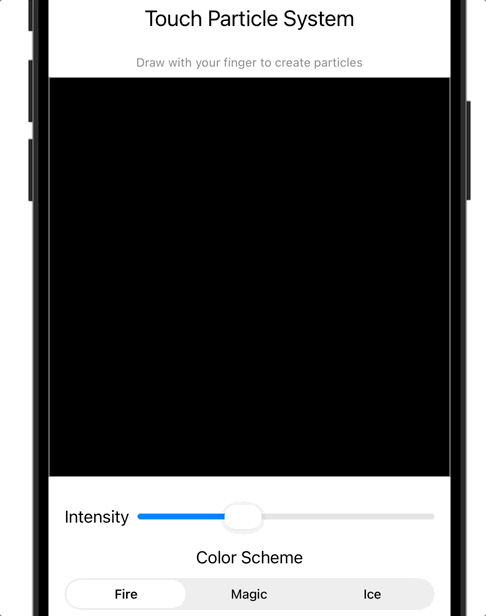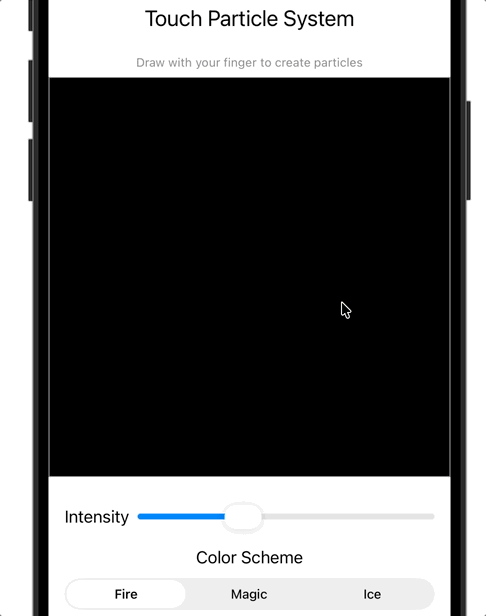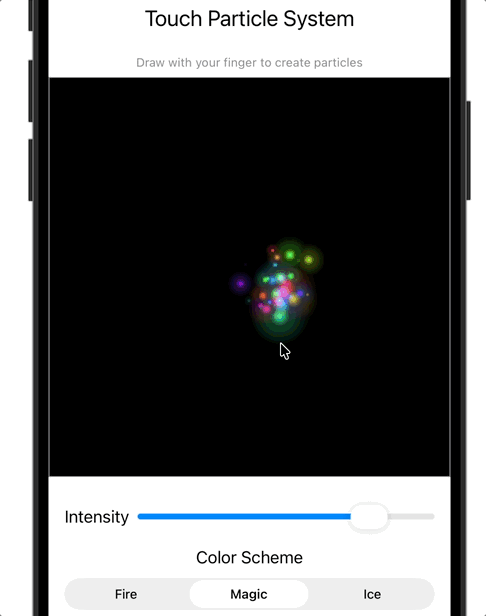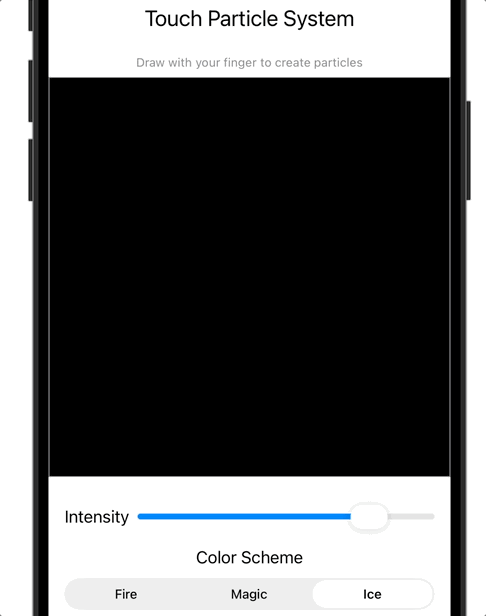
Touch Particle System Example

Create a touchParticles shader that spawns particles at touch location with random properties using noise functions. Think about this as a magic drawing board.

Requirements:

Particles spawn at touch position with random velocities
Each particle has unique size, color variation, and lifetime
Particles fade out smoothly over time
Use noise for organic movement patterns
Visual: Like sparkles or fairy dust following your finger

SwiftUI Template:

struct TouchParticleView: View {
    @State private var touchPosition = CGPoint(x: 0.5, y: 0.5)
    @State private var isTouching = false
    @State private var timeValue: Float = 0.0
    @State private var particleIntensity: Float = 1.0
    @State private var colorScheme: Float = 0.0
    
    let timer = Timer.publish(every: 1/60.0, on: .main, in: .common).autoconnect()
    
    var body: some View {
        VStack {
            Text("Touch Particle System")
                .font(.title2)
                .padding()
            
            Text("Draw with your finger to create particles")
                .font(.caption)
                .foregroundColor(.secondary)
            
            GeometryReader { geometry in
                Rectangle()
                    .fill(Color.black)
                    .visualEffect { content, proxy in
                        content.colorEffect(ShaderLibrary.touchParticles(
                            .float2(proxy.size),
                            .float(timeValue),
                            .float2(Float(touchPosition.x), Float(touchPosition.y)),
                            .float(isTouching ? 1.0 : 0.0),
                            .float(particleIntensity),
                            .float(colorScheme)
                        ))
                    }
                    .gesture(
                        DragGesture(minimumDistance: 0)
                            .onChanged { value in
                                isTouching = true
                                touchPosition = CGPoint(
                                    x: value.location.x / geometry.size.width,
                                    y: value.location.y / geometry.size.height
                                )
                            }
                            .onEnded { _ in
                                isTouching = false
                            }
                    )
            }
            .frame(height: 400)
            .border(Color.gray, width: 1)
            
            VStack(spacing: 15) {
                HStack {
                    Text("Intensity")
                    Slider(value: $particleIntensity, in: 0.5...2.0)
                }
                
                Picker("Color Scheme", selection: Binding(
                    get: { Int(colorScheme) },
                    set: { colorScheme = Float($0) }
                )) {
                    Text("Fire").tag(0)
                    Text("Magic").tag(1)
                    Text("Ice").tag(2)
                }
                .pickerStyle(SegmentedPickerStyle())
            }
            .padding()
        }
        .onReceive(timer) { _ in
            timeValue += 1/60.0
        }
    }
}

🔥 Black Friday — 50% OFF

Want the Challenges Solutions?

Get the full Xcode project with solutions to all challenges, bonus examples, and clean, runnable code.

Get 50% Off Now →

Validation Questions

Why can't shaders use traditional random() functions?
- Answer: Shaders execute the same code for every pixel simultaneously. A traditional random() would either return the same value for all pixels (defeating the purpose) or different values each frame (causing flickering). Shaders need deterministic functions that produce consistent "random" values based on position.
What makes the hash function fract(sin(dot(st, float2(12.9898,78.233))) * 43758.5453) work?
- Answer: The dot product combines 2D coordinates into a single value. Sin() creates non-linear variation. The large multiplier (43758.5453) amplifies tiny differences in the sine values. Fract() keeps the result in 0-1 range. The specific numbers aren't magical - they just produce good distribution.
Why do we use multiple octaves of noise?
- Answer: Natural textures have detail at multiple scales. Mountains have overall shape (low frequency) plus smaller rocks and details (high frequency). Each octave adds a different scale of detail, with decreasing amplitude to prevent high-frequency noise from dominating.
What's the difference between value noise and gradient noise?
- Answer: Value noise interpolates between random values at grid points, creating a smooth but somewhat blobby result. Gradient noise (Perlin) interpolates between random gradients/directions at grid points, creating more natural-looking variation with better properties for animation.
How do you ensure noise-based animations don't flicker?
- Answer: Use smooth, continuous movement through noise space (e.g., noise(uv + time * speed)) rather than using time to seed the randomness. The noise function itself should be continuous and smooth. Avoid recalculating random seeds every frame.
Why is simplex noise better than classic Perlin noise?
- Answer: Simplex noise uses triangular grids (simplexes) instead of square grids, requiring fewer calculations (3 corners vs 4 in 2D). It has better computational complexity, no directional artifacts, and scales better to higher dimensions. The visual quality is similar but performance is significantly better.

Further Exploration

Worley Noise: Cellular patterns based on distance to random points
Blue Noise: Even distribution without clumping
Curl Noise: Divergence-free noise for fluid simulation
Domain Warping: Using noise to distort noise for organic effects

Next Chapter Preview: You've learned to add organic randomness to your shaders. Chapter 7 introduces smoothstep and anti-aliasing techniques to create professional-quality edges and transitions. You'll understand why pixelated edges scream "amateur" and how to achieve the silky-smooth gradients that make viewers lean in closer.